Alexander Genser
Dynamic congestion pricing for urban transportation networks
Predicting dynamic region tolls for a multi-region transportation network with deep learning
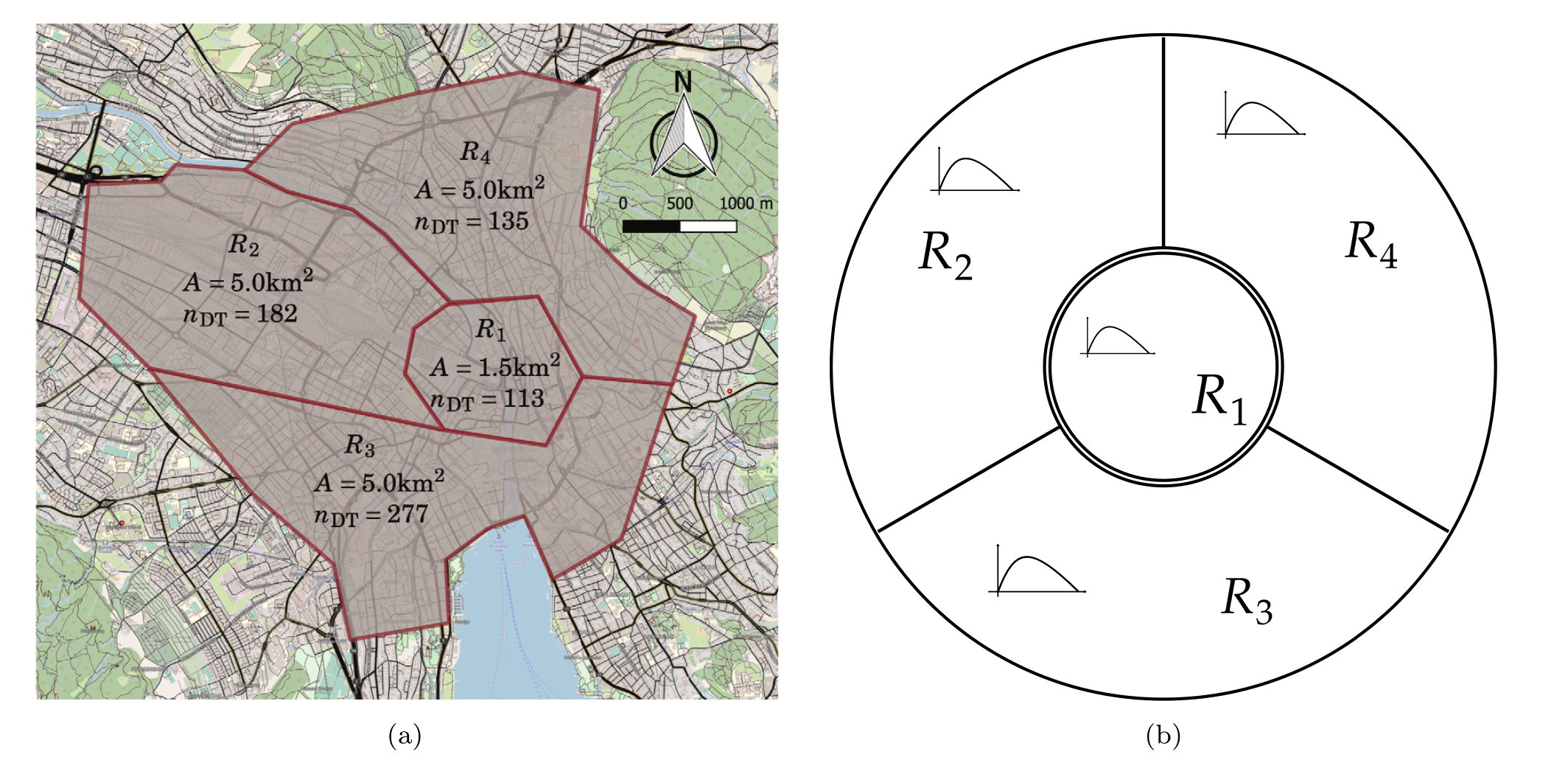
Problem description
Full paper: | Implementation:
In the face of growing urban populations, traffic congestion has emerged as a pressing challenge, hindering the efficient movement of people and goods. While various traffic management strategies have been employed to tackle this issue, congestion pricing stands out as a promising solution with the potential to significantly reduce congestion, internalize external costs, and improve overall traffic performance.
Conventional methods for implementing congestion pricing, such as link-based pricing, often face practical limitations due to high infrastructure investments and regulatory hurdles. To overcome these challenges, this research focuses on developing a macroscopic congestion pricing approach, which consider the network as a whole rather than individual links. This paper presents a novel framework for optimal macroscopic congestion pricing, employing supervised machine learning to optimize tolling strategies in a multi-region network.
Contributions
- The formulation of an efficient and linear program for real-time DSO optimization significantly enhances the computational efficiency and scalability of the framework.
- The development of MLN network models provides a powerful tool for predicting user route choices and capturing complex behavioral patterns, enabling the framework to respond to dynamic traffic conditions with greater precision.
- The derivation of demand-specific pricing functions tailored to each region ensures that tolls are effectively utilized to manage congestion and optimize network performance.
Findings
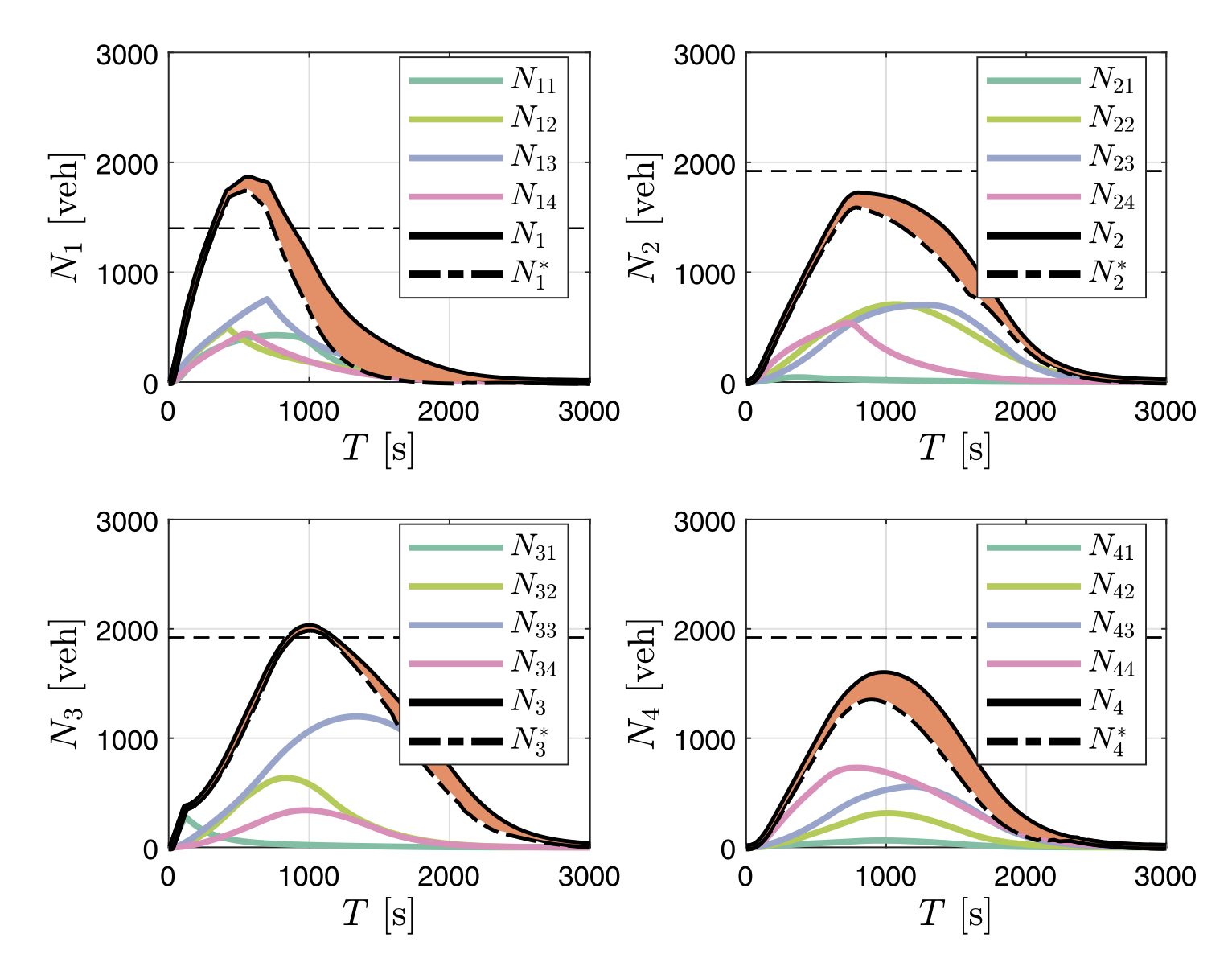
Dynamic system optimum (DSO) is a method for optimizing traffic flow by dynamically adjusting the splitting rates between different routes. Compared to the deterministic route choice (DRC) approach, which assumes fixed splitting rates, DSO can significantly improve network performance. In a numerical experiment based on a model of the city of Zurich, DSO was shown to result in a 21.93%, 8.77%, 4.39%, and 11.45% improvement in travel time saving (TS) for regions 1, 2, 3, and 4, respectively.
Machine learning (ML) can be used to effectively predict generalized trip costs in a multi-region network. A novel ML model was trained on a data set of historical traffic patterns and splitting rates, and it was able to predict generalized trip costs with an average mean absolute error (MAE) of 1.38%. This accuracy allows the ML model to be used to guide the DSO approach in optimizing traffic flow.
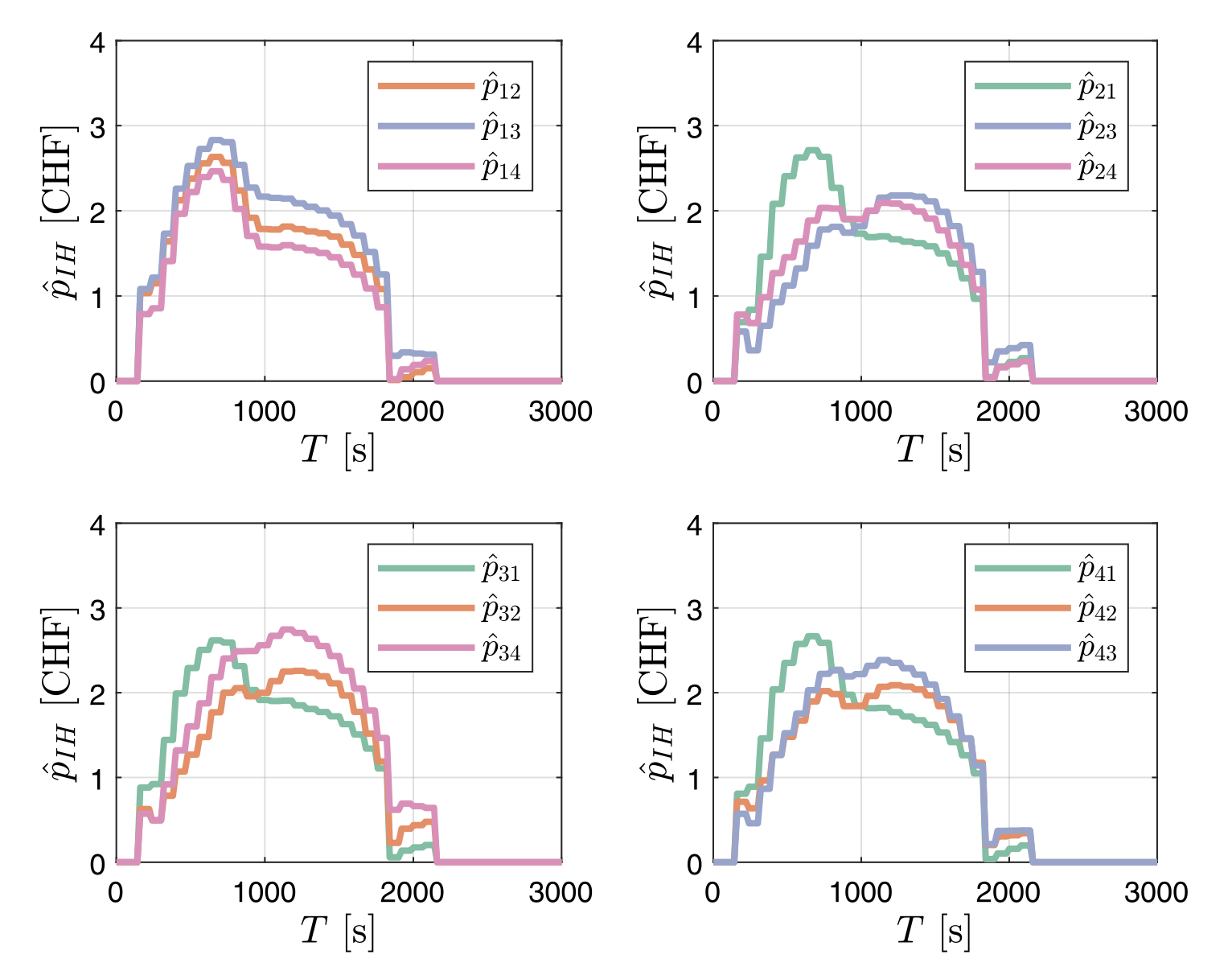
Optimal dynamic pricing (OP) is a method for dynamically adjusting tolls at the network boundaries to incentivize users to choose routes with lower generalized trip costs. In the numerical experiment, OP was shown to further improve network performance by an additional 14.32%, 12.15%, 5.23%, and 13.47% for regions 1, 2, 3, and 4, respectively. This additional improvement is due to the fact that OP can directly respond to real-time changes in traffic conditions.
The proposed methodology is robust to noisy data and can be used with large data sets. The ML model can still predict generalized trip costs with an average MAE of 1.40% when trained on a data set with additive white Gaussian noise. The OP approach also shows effectiveness when applied to a data set with 200 simulations. Overall, the proposed methodology for dynamic macroscopic congestion pricing is a promising approach for improving network performance and reducing congestion in urban areas. The methodology is based on a combination of DSO, ML, and OP, and it has been shown to be effective in a numerical experiment based on a model of the city of Zurich. The methodology is also robust to noisy data and can be applied to large data sets.
References
[1] Genser, Alexander, and Anastasios Kouvelas. "Dynamic optimal congestion pricing in multi-region urban networks by application of a Multi-Layer-Neural network." Transportation Research Part C: Emerging Technologies 134 (2022): 103485.
[2] Sirmatel, Isik Ilber, and Nikolas Geroliminis. "Economic model predictive control of large-scale urban road networks via perimeter control and regional route guidance." IEEE Transactions on Intelligent Transportation Systems 19.4 (2017): 1112-1121.
[3] Gu, Ziyuan, et al. "Optimal distance-and time-dependent area-based pricing with the Network Fundamental Diagram." Transportation Research Part C: Emerging Technologies 95 (2018): 1-28.