Traffic state estimation with DNN

Combining traditional traffic models with deep learning techniques.

Problem description

Full paper: | Implementation:

Research interest in understanding and estimating traffic conditions on highway networks has been vivid for over 50 years. Traffic estimation methods aim to derive traffic variables based on modeling, observation, or both. In the era of intelligent transportation systems, efficient traffic monitoring can help develop robust traffic control schemes to facilitate mobility, reduce congestion and emissions, and ensure safety. In addition, the abundance of portable, accurate, and low-cost sensors at the infrastructure, vehicle, or people level is expected to generate large amounts of data that can be used for traffic estimation solutions.

Parametric traffic models such as CTM [1] or METANET [2] are computationally inexpensive and capture the traffic dynamics in space and time to a reasonable extent. However, they need significant efforts for proper calibration, and their performance drops when applied on large networks due to highly complex dynamics and implementation difficulties. Recently, the interest in data-driven traffic estimation methodologies has been increasing. Data observations provide accurate estimates if adequately used. At the same time, advanced deep learning strategies can capture higher non-linear traffic dynamics than traffic models. However, a significant problem to date is data scarcity. Observations are usually available at specific parts of the networks, with low penetration rates, and their reporting frequency is often inconsistent. The data assimilation family of developments inspires the basic idea of the proposed work. It aims to exploit the best of both worlds, models, and data by developing a physics-informed deep learning framework for traffic estimation on large freeway networks. Traditional traffic models capture well the traffic dynamics in space and time. On the other hand, observations provide a significantly better representation of the traffic dynamics, but their estimates are confined to space at the measurement place. At the same time, a deep learning framework can, in theory, study the discrepancies between models and observation and identify error patterns between the two worlds. The assumption in this idea is that error discrepancies between models and data can be identified in a large number of patterns over a network. Therefore, a systematic study of these patterns can help us provide reasonable estimates locally, i.e., with data availability and globally in the network.

Contributions

  • A framework that implements a bidirectional Long-Short-Term-Memory (biLSTM) neural network to estimate the traffic state.
  • A physics-informed methodology based on the concept of triplets to capture spatial-temporal dynamics.
  • Preliminary results of a case study that utilizes a stretch of the Antwerp ring-road network and seem promising compared to data assimilation approaches.

Findings

The presented framework aims to estimate traffic states on a freeway network with on- and off- ramps by combining the strengths of traditional traffic models and deep learning techniques. Our approach, therefore, utilizes traffic state estimates from traffic models and measurement data that, e.g., various established and fixed installed sensors or moving Connected and Automated Vehicles (CAV) provide. Figure 1 depicts the proposed framework with its components. As a starting point for our method, traffic states from traditional traffic models serve as input. The utilized model(s) (e.g., CTM, METANET) are members of the model collection. The set can hold estimates from either one or multiple sources (e.g., Kalman Filters, Particle Filters). The generic approach allows for incorporating different traffic model estimate combinations to assess and tune performance. The provided estimates are denoted as the traffic density ρi(k) and space mean speed vi(k) of a network segment i at discretized time k. A network consists of I segments and i ∈ I. ri(k) denotes the inflow at an on-ramp connected to segment i. si(k) denotes the split of traffic flow that exits the freeway via an off-ramp. Due to the prior estimation of traffic density and space mean speed with a traffic model, the quantities serve in Figure 1 as an input to the estimation framework proposed in the following.

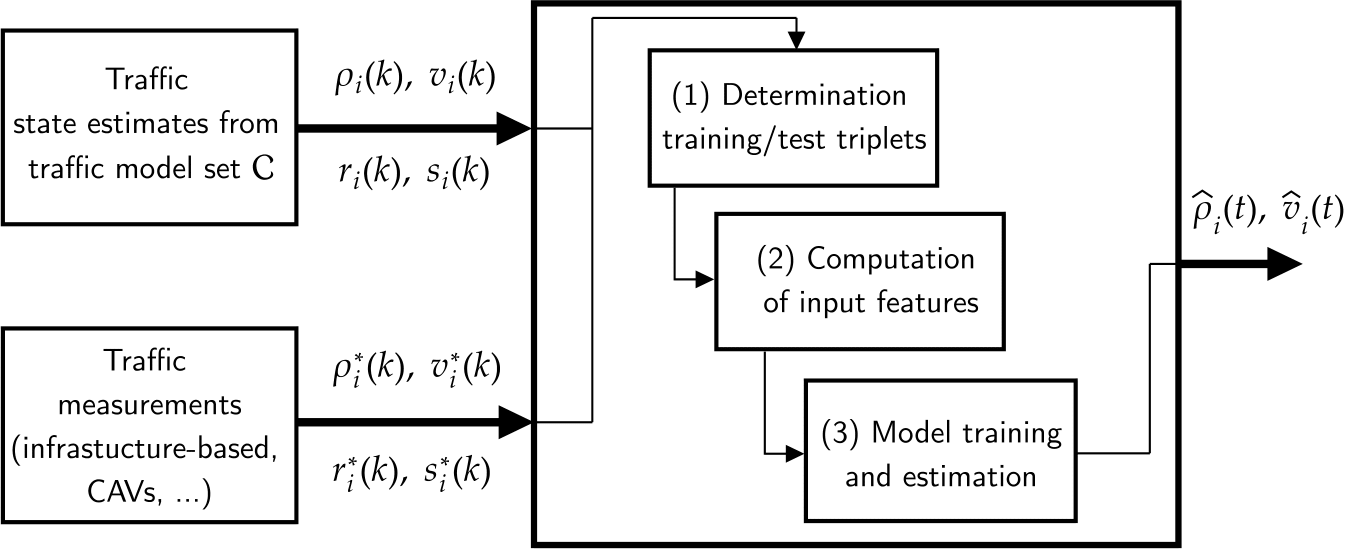
framework traffic state estimation
Figure 1: Framework description to determine traffic state estimates.

The second set of inputs in Figure 1 constitute measurements from sparsely available sensor data in the network. Such inputs can either be determined from sensors implemented at a fixed location (e.g., loop detectors, Bluetooth sensors, cameras) or, in a Vehicle-to-Infrastructure (V2I) environment, from moving CAVs that broadcast the traffic-related information. In this work, the measurements for traffic density ρ∗j(k) and space mean speed v∗j(k) are already aggregated for a segment i. Also, measurements for inflow at an on-ramp and the split of exiting flow, r∗i(k) and s∗i(k), are available. The asterisk denotes measurement quantities. The two different sets of inputs (traffic estimates from traditional traffic models and measurement data) are then utilized in block (1) (Figure 1). To determine an estimation model, we introduce training and testing triplets. The concept of triplets is defined as three contiguous seg- ments in a freeway network denoted with the indices i − 1, i, i + 1. The idea of using triplets is to capture the error correlations between neighboring parts in the network; i.e., the spatial com- ponent of traffic dynamics is considered during model training.

For the training and testing of a model candidate, the input data needs to be split into training and testing data. We utilize the segments with sparse available measurement data to compute training triplets. A training triplet strictly holds the available measurements in segment i (i.e., always the middle segment). Consequently, we utilize all traffic model estimates for i − 1, i, and i + 1 as input and define the measurements in segment i as a target. This approach allows for solving a supervised regression problem to mitigate the error from traffic model estimates. All other triplets that do not hold measurements for segment i are denoted as testing triplets. In block (2), the input features are computed for model training. To ensure a consistent input feature vector, all on-ramp and off-ramp features are present, regardless of infrastructure design. Details about this procedure can be found in [3].

After feature engineering, the final set of training data is utilized to train a biLSTM model to predict the traffic density in unobserved segments. The prediction accuracy is evaluated with the Mean Absolute Error (MAE) and Root Mean Square Error (RMSE) against the application of a Unscented Kalman Filter (UKF). Again [3] provides the determined architecture and details about training and testing.

The case study is based on a stretch from a 120km freeway ring road in Antwerp, Belgium. The data set is based on a calibrated representation of the network in Aimsun. The simulation scenario represents three hours, where the first hour corresponds to the loading phase (20% of peak hour demand) and the last hour to the unloading phase (20% of peak hour demand). The network stretch is represented by 17 multi-lane segments, three on-ramps, and one off-ramp. Four segments hold measurements (CAV measurements with a penetration rate of 50%) of traffic density and space mean speed. For the other 12 segments, no measurements are available. In this work, we utilize the well-known model METANET as the traditional traffic model. First, the candidate is applied to the segmented freeway stretch for the prior traffic state estimation. This step allows the computation of traffic density and space mean speed for all 17 segments. To prove our concept, we focus this work on estimating traffic density. Note that the framework also allows training a model for space mean speed estimation or both quantities at a time.

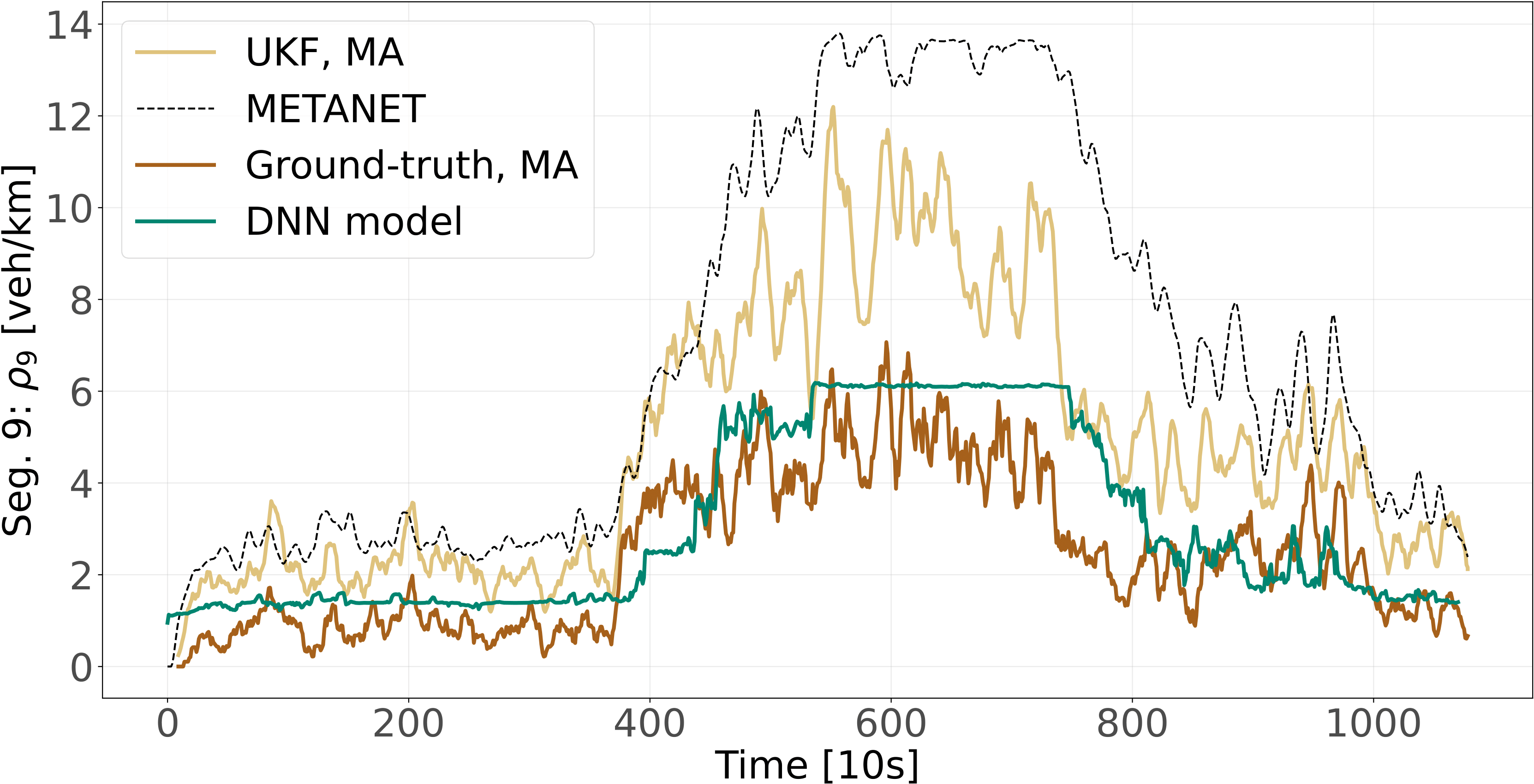
Figure 2 showcases estimation results for segments 9. A qualitative inspection of METANET estimates (dashed black) shows an overestimated traffic density for the loaded network between 4000s and 8000s in segment 9. The UKF result (in yellow) shows a slight overestimation of traffic density during loading and unloading and a significant overestimation during 4000s and 8000s. The application of the biLSTM model allows for a reduction of the MAE error by 61% from 2.39 veh/km to 0.93 veh/km (the RMSE decreases by 56%). The estimated traffic density shows a good fit throughout the investigated period compared to the ground-truth (in brown). Table 1 also shows a reduction of the RMSE for segment 12 from 2.03 veh/km to 1.43 km/veh, corresponding to an improvement of 30%. Out of 13 testing triplets, 8 show similar results for MAE and RMSE, where the biLSTM model outperforms the UKF and the traditional traffic model. Nevertheless, Table 1 also shows testing triplets where the UKF outperforms the biLSTM model. For example, segment 16 shows an RMSE of 1.45 veh/km and 2.48 veh/km, respectively, corresponding to a performance loss of 71%. An analysis of the METANET estimates (i.e., the input for the biLSTM model) shows a substantial overestimation by the traffic model, which is likely to cause modest results for biLSTM.

result traffic state estimation
Figure 2: Estimation results of biLSTM model for traffic density of segment 9. Comparison with METANET, UKF (moving average with a window of 10), and ground-truth simulation data (moving average with a window of 10).

Table 1: Performance assessment of UKF and biLSTM on training (highlighted in green) and testing triplets (highlighted in blue) with RMSE, respectively.
Model Seg. 0 Seg. 1 Seg. 2 Seg. 3 Seg. 4 Seg. 5 Seg. 6 Seg. 7 Seg. 8
UKF 1.43 1.29 1.04 0.37 0.28 2.45 1.34 1.14 1.04
biLSTM 1.15 1.04 1.04 0.89 0.77 1.25 1.33 1.33 1.40
Seg. 9 Seg.10 Seg. 11 Seg. 12 Seg. 13 Seg. 14 Seg. 15 Seg. 16
UKF 2.72 0.79 0.86 2.03 2.51 2.25 1.98 1.45
biLSTM 1.20 1.10 0.93 1.43 2.31 2.22 2.23 2.48

The proposed work studies a flexible framework for traffic state estimation of freeway networks by exploiting deep learning techniques. The work allows for fusing traffic model estimates and available measurement data. The methodology allows one to (a) train and assesses the model on segments where measurements are and (b) estimate the traffic state in segments where no data is available. Results highlight that the framework outperforms traditional traffic models.

References

[1] Daganzo, C. F. (1995). The cell transmission model, part II: network traffic. Transportation Research Part B: Methodological, 29(2), 79-93.

[2] Papageorgiou, M., Blosseville, J. M., & Hadj-Salem, H. (1990). Modelling and real-time control of traffic flow on the southern part of Boulevard Peripherique in Paris: Part I: Modelling. Transportation Research Part A: General, 24(5), 345-359.

[3] Genser, A., Makridis, M., & Kouvelas, A. (2022). Exploiting deep learning and traffic models for freeway traffic estimation. In 4th Symposium on Management of Future Motorway and Urban Traffic Systems (MFTS 2022).